残差。我们常利用计算残差来评判计算是否达到收敛。那么什么是残差?
残差的概念来自于迭代法,指的是同一物理量在两次迭代之间的变化量。度量残差的方法很多,比如说计算差值、均方根等。
1 迭代法中的残差
下面这段代码利用松弛迭代法求解线性方程组,并输出三个未知量x1,x2及x3的残差变化曲线。
# -*- coding: utf-8 -*-#
import matplotlib.pyplot as plt
import numpy as np
def f(x1, x2, x3, count, w):
it = np.arange(1,count,1)
count =[]
x1r = []
x2r = []
x3r = []
for item in it:
y1 = x1-w*(x1-0.1*x2-0.2*x3-7.2)
y2 = x2-w*(-0.1*y1+x2-0.2*x3-8.3)
y3 = x3-w*(-0.2*y1 -0.2 *y2+x3-8.4)
if (max(abs(y1-x1), abs(y2-x2), abs(y3-x3)) < 0.00001):
# 设定精度为0.00001
print('最终的计算结果为%s、%s和%s' % (y1, y2, y3))
break;
else:
print('第%s次迭代的计算结果为%s、%s和%s' % (item, y1, y2, y3))
x1r.append(abs(y1 - x1))
x2r.append(abs(y2 - x2))
x3r.append(abs(y3 - x3))
count.append(item)
x1,x2,x3 = y1,y2,y3
plt.plot(count,x1r,'r',label='x1')
plt.plot(count,x2r,'b',label='x2')
plt.plot(count,x3r,color='green',label='x3')
plt.yscale('log')
plt.xlabel('Iteration')
plt.ylabel('Residual(log)')
plt.legend()
plt.show()
f(15,15,8,1000,0.5)前面的文章中,采用递归来迭代计算,这里采用循环来定义迭代过程。
重要的代码在这里:
if (max(abs(y1-x1), abs(y2-x2), abs(y3-x3)) < 0.00001):
print('最终的计算结果为%s、%s和%s' % (y1, y2, y3))
break;这几行代码定义了残差为0.00001,当所有物理量的变化量低于该阈值时,计算停止。
上面的代码经过22次迭代达到收敛,输出的残差变化曲线如下图所示。
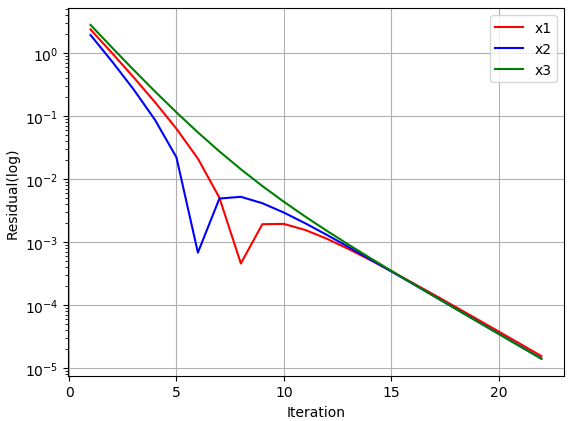
下图是改用松弛因子1.0计算的残差曲线。计算在迭代6步后达到收敛。
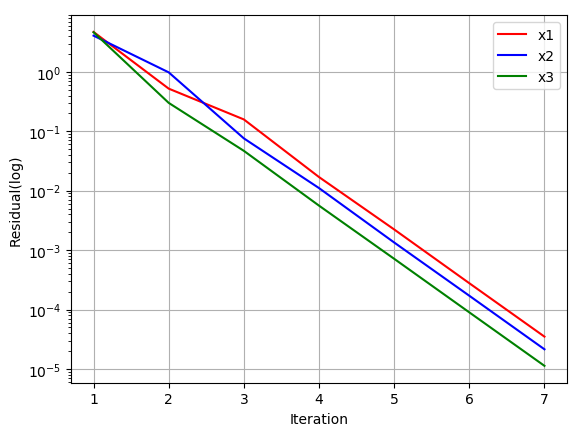
下图利用松弛因子1.5进行计算得到的残差图。计算在迭代21次后达到收敛。
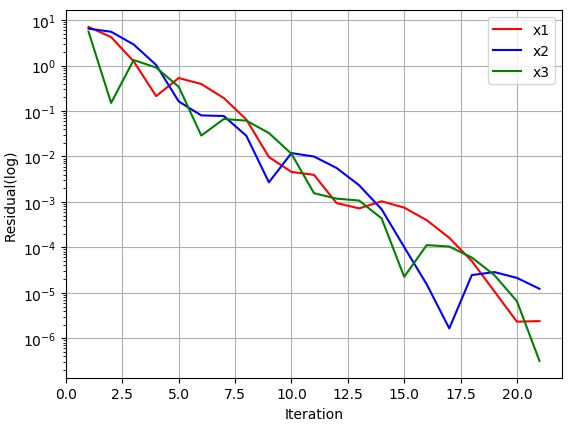
需要注意的是:
-
上面采用的三种不同的亚松弛因子(0.5,1.0,1.5)进行计算,最终均收敛值1e-5,虽然残差曲线不同,但最终获取的计算结果是相同的。
-
残差降低到收敛标准,只能表示计算收敛,但无法证明结果正确与否。但是能确定的是,计算没有达到收敛,其结果肯定是不正确的。
2 Fluent中残差设置
在Fluent软件中,双击模型树节点Monitor > Residual即弹出残差设置对话框,如下图所示。
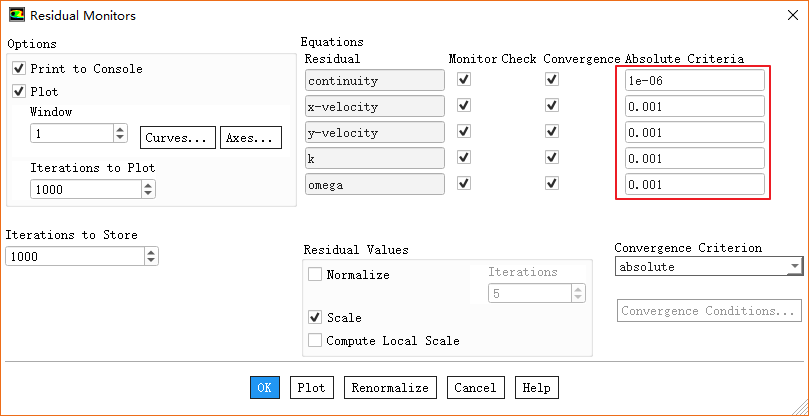
在该对话框中,用户可以设定每一个物理量的残差标准。
关于在Fluent中残差设置的一些经验:
二维计算模型通常设置残差低于1e-5
能量方程残差通常低于1e-6
对于复杂计算模型,残差并非判断收敛的唯一标准

注:本文部分内容来自连载《小白学CFD》,转载请务必保持文章完整性!
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册